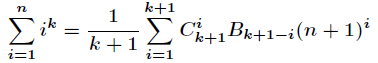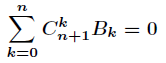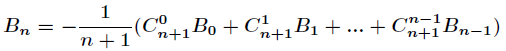51Nod - 1228 序列求和（自然数幂和+伯努利数）-白红宇

51Nod - 1228 序列求和（自然数幂和+伯努利数）

阅读量：6757 次

发布时间：2019-06-26

本文共 1318 字，大约阅读时间需要 4 分钟。

Description

T(n) = n^k，S(n) = T(1) + T(2) + ...... T(n)。给出n和k，求S(n)。

例如k = 2，n = 5，S(n) = 1^2 + 2^2 + 3^2 + 4^2 + 5^2 = 55。

由于结果很大，输出S(n) Mod 1000000007的结果即可。

Input

第1行：一个数T，表示后面用作输入测试的数的数量。（1 <= T <= 5000)

第2 - T + 1行：每行2个数，N, K中间用空格分割。(1 <= N <= 10^18, 1 <= K <= 2000)Output共T行，对应S(n) Mod 1000000007的结果。

Sample Input

35 34 24 1

Sample Output

分析

求自然数的幂和，有一个基于伯努利数的公式。

于是线性处理出每一项，那么每个case就是线性求解了。

伯努利数怎么计算呢？

首先B0=1，然后有

将Bn提取出来，得到

这样就能递推伯努利数了。

#include 
     
      #include 
      
       #include 
       
        #include 
        
         #include 
         
          #include 
          
           #include 
           
            #include 
            
             #include 
             
              #include 
              
               #include 
               #include 
                
                 #include 
                 
                  #include 
                  
                   using namespace std;typedef long long ll;typedef unsigned long long ull;#define ms(a, b) memset(a, b, sizeof(a))#define pb push_back#define mp make_pair#define pii pair
                   
                    #define eps 0.0000000001#define IOS ios::sync_with_stdio(0);cin.tie(0);#define random(a, b) rand()*rand()%(b-a+1)+a#define pi acos(-1)const ll INF = 0x3f3f3f3f3f3f3f3fll;const int inf = 0x3f3f3f3f;const int maxn = 2000 + 100;const int maxm = 200000 + 10;const int mod = 1e9+7;ll C[maxn][maxn],B[maxn],inv[maxn];inline ll add(ll a){ if(a>=mod) a-=mod; return a;}void init(){ C[0][0]=1; for(int i=1;i